156
Goniometrie – Gönner
Anmerkung: Fortsetzung des Artikels 'Goniometer'
malenwinkel der betreffenden Kante ergeben. Der gespiegelte Gegenstand sowie das beobachtende Auge müssen beide während der Messung dieselbe Richtung
beibehalten, damit der reflektierte Lichtstrahl keinen andern Weg einschlägt; sowohl das einfallende wie das reflektierte Licht geht daher bei den bessern
neuern Instrumenten durch je ein Fernrohr (Einlaß- und Okularfernrohr). Die zu messende Krystallkante muß justiert, d. h. senkrecht sein zur Ebene des
Limbus und zu der durch die Fernrohre gelegten Ebene, andererseits muß sie centriert sein, d. h. in der Verlängerung der Limbusachse liegen. Die zwar
verhältnismäßig ebenen, aber matten Krystalloberflächen pflegt man, um eine Spiegelung derselben zu bewirken, aushilfsweise mit dünnen Glasplättchen zu
bedecken. Bei den meisten ältern Instrumenten steht der Teilkreis vertikal (wie in der Figur), kommt also die zu messende Kante horizontal zu liegen
(System von Wollaston). Neuerdings giebt man den G. mit horizontalem Teilkreis und senkrechter Drehungsachse (System von Malus) häufig den Vorzug. Das G.
von Wollaston wurde durch Mitscherlich und B. von Lang, dasjenige von Malus, der auch die Visierrichtung durch das Fernrohr mit Fadenkreuz fixierte, durch
Babinet und in neuester Zeit durch Websky verbessert. – Vgl. Groth, Physikalische Krystallographie (2. Aufl., Lpz. 1885).
Goniomĕtrie, Winkelmessung, die Lehre von den
Goniometrischen Funktionen (s. d.); dann auch die praktischen Vorschriften über die Messung von
Winkeln. Man gebraucht zur praktischen Winkelmessung verschiedene, mit eingeteilten Kreisen versehene Instrumente, z. B. die Bussole, den Theodolit,
den Spiegelsextanten, das Reflexionsgoniometer. Zur Berechnung von Winkeln gelangt man durch Benutzung von Winkelfunktionen
(s. Goniometrische Funktionen). Daher ist G. auch ein Abschnitt der Trigonometrie und der mathem. Analysis. – Vgl. Meyer, Lehrbuch
der G. (Stuttg. 1886).
Textfigur:
Goniometrische Funktionen, das Hilfsmittel, aus den Bestimmungsstücken eines Dreiecks die übrigen Stücke durch Rechnung zu
finden; bilden dadurch die Grundlage der Trigonometrie (s. d.). Die G. F. stellen Beziehungen dar zwischen den Winkeln und den Seiten
eines rechtwinkligen Dreiecks, und zwar hat man bei Aufstellung dieser Beziehungen den Umstand benutzt, daß durch die Veränderung der spitzen Winkel eines
solchen Dreiecks eine ganz bestimmte Änderung der Verhältnisse je zweier Seiten eintritt, sodaß man diese Seitenverhältnisse als Funktionen der Winkel
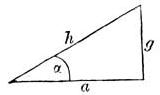
betrachtet und mit dem Namen G. F. oder Winkelfunktionen belegt. In beistehender Figur ist ein rechtwinkliges Dreieck
dargestellt, in welchem ein spitzer Winkel mit α, die Hypotenuse mit h, die dem Winkel α anliegende Kathete mit a, die ihm gegenüberliegende mit g
bezeichnet ist. Man nennt nun:
| das | Verhältnis | g | den Sinus von α (sin α), |
| h |
| " | " | a | den Kosinus von α (cos α), |
| h |
| " | " | g | die Tangente von α (tan α od. tg α), |
| a |
| " | " | h | die Kosekante von α (cosec α), |
| g |
↔
| das | Verhältnis | h | die Sekante von α (sec α), |
| a |
| " | " | a | die Kotangente von α (cot α). |
| g |
Zwischen diesen G. F., von denen meist nur die drei ersten gebraucht werden (die drei letzten sind die reciproken Verhältnisse der drei ersten), finden
folgende beiden Beziehungen statt:
| | sin α = tg α • cos α | | und |
| | sin2α + cos2α = 1, | | |
durch welche es unter Zuhilfenahme der erwähnten Reciprocität möglich ist, jede der sechs G. F. des Winkels α aus jeder andern zu berechnen. Für die
Funktionen von Winkelsummen und -Differenzen gilt:
| | sin (α ± β) = | sin α • cos β ± cos α • sin β |
| | cos (α ± β) = | cos α • cos β ± sin α • sin β |
| | tg (α ± β) = | tg α ± tg β | |
| | 1 + tg α • tg β | |
Die G. F., die auch einen Gegenstand der allgemeinen Funktionentheorie darstellen, lassen sich in Reihen entwickeln.
Es ist
| sin x = x – | x3 | + | x5 | – | x7 | + ..., |
| 3! | 5! | 7! |
| cos x = 1 – | x2 | + | x4 | – | x6 | + ..., |
| 2! | 4! | 6! |
| tg x = x + | x3 | + | 2x5 | + | 17x7 | + | 62x9 | + ..., |
| 3 | 3•5 | 32•5•7 | 33•5•7•9 |
worin ! das Zeichen für Fakultät (s. d.) ist.
Die Umkehrung der G. F. sind die Cyklometrischen Funktionen (s. d.).
Gonionds, poln. Goniądz, Flecken im Kreis Bjelostok des russ. Gouvernements Grodno, 60 km
nordwestlich der Stadt Bjelostok, links am höhern Ufer des schiffbaren Bobr, an der Grenze Polens, hat (1885) 4345 E., Post, kath. Kirche, Synagoge,
Flußhafen, lebhaften Handel. Am rechten, niedrigern Ufer liegt das Dorf Ossowez, Station der Eisenbahn
Brest-Litowsk-Grajewo. Beide Ufer sind befestigt. Die Festung, gewöhnlich Ossowez genannt, ist eine Festung dritter Klasse und sichert das für
Truppensammlungen wichtige Bjelostok.
Gonitis (grch.), Kniegelenkentzündung.
Gonne, Friedrich, Maler, geb. 30. Mai 1813 zu Dresden, bildete sich seit 1834 an der Akademie daselbst und bereiste seit 1837
Europa. Seit 1857 ist er Professor und Mitglied der Akademien in Dresden und Amsterdam. Von seinen Genrebildern sind hervorzuheben: Der Judaskuß,
Bajazzo hinter den Coulissen, Verfehltes Leben, Brennende Erinnerungen (1869; Kunsthalle in Hamburg), Die Konvenienzheirat, Des Räubers Reue (1883),
Ein Bauernfänger in einer Dorfschenke (1887). Außerdem malte er Bildnisse (Porträt des Königs Johann von Sachsen, im Rathaus zu Leipzig) und einige
Altarbilder (Die Jünger in Emmaus für die Kirche in Schellenberg). Er schrieb: «Flüchtige Blicke in Natur und Kunst» (Dresd. 1869), «Das Gleichgewicht
in der Bewegung» (ebd. 1882).
Gönner, Nikol. Thaddäus von, Jurist und Publizist, geb. 18. Dez. 1764 zu Bamberg, erhielt teils hier, teils auf der Universität
zu Göttingen seine wissenschaftliche Bildung. Nach der Rückkehr
Anmerkung: Fortgesetzt auf Seite 157.
